Problem 1:
Exhibit both a partial ordering and a simple ordering on the set of complex numbers.
Solution I:
Recall the definition of a partial ordering: A binary relation R on a set M is said to be a partial ordering (and the set M itself is said to be partially ordered) if:
(i) R is reflexive (aRa for every 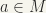 ) (ii) R is transitive (aRb and bRc together imply aRc) (iii) aRb and bRa together imply
) (ii) R is transitive (aRb and bRc together imply aRc) (iii) aRb and bRa together imply  (anti symmetric).
(anti symmetric).
Recall the definition of a simple ordering or totally ordered or (just) ordered set: a set M is said to be ordered if it is a partially ordered set and if, given any two distinct elements  , either
, either 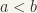 or
or 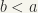 .
.
Let us consider the following relation R on the set of complex numbers, C:
consider any two elements 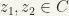 such that
such that  and
and  . We define a relation
. We define a relation 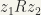 if and only if
if and only if  and
and  . Clearly, this is both a partial ordering on C as well as total ordering on C.
. Clearly, this is both a partial ordering on C as well as total ordering on C.
Now consider the following relation K on the set of complex numbers:
We define the relation K as:  if and only if
if and only if  where
where 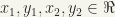 . Clearly, if any one of
. Clearly, if any one of  or
or 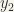 is zero, then the complex numbers
is zero, then the complex numbers 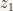 and
and 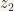 are non-comparable. So this could be a partial ordering but not a total ordering on the set of complex numbers.
are non-comparable. So this could be a partial ordering but not a total ordering on the set of complex numbers.
Problem 2:
What is the minimal element of the set of all subsets of a given set X partially ordered by set inclusion. What is the maximal element?
Solution 2:
Recall the definition: An element “a” of a partially ordered set is said to be maximal if 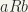 implies
implies  and minimal if
and minimal if 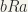 implies b=a.
implies b=a.
Note that in the above definition, element “a” is our given/chosen element to be compared with other elements of the set. So, clearly, if the partial ordering is set inclusion, the minimal element is the null set  and the maximal element is the given set X itself.
and the maximal element is the given set X itself.
Problem 3:
A partially ordered set M is said to be a directed set if, given any two elements  , there is an element
, there is an element  such that
such that  and
and  . Are the following partially ordered sets directed sets also ?
. Are the following partially ordered sets directed sets also ?
PS: in the above we use the notation 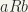 or equivalently,
or equivalently,  to mean one and the same thing.
to mean one and the same thing.
Question 3a: Any set M can be trivially partially ordered by setting  if and only if
if and only if  .
.
Answer 3a: Clearly, this is a trivial directed set.
Question 3b: Let M be the set of all continuous functions  defined in a closed interval
defined in a closed interval ![[\alpha, \beta]](https://s0.wp.com/latex.php?latex=%5B%5Calpha%2C+%5Cbeta%5D&bg=%23f6f5ed&fg=222222&s=0&c=20201002) . Then, we get a partial ordering by setting
. Then, we get a partial ordering by setting  if and only if
if and only if 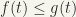 for every
for every ![t \in [\alpha, \beta]](https://s0.wp.com/latex.php?latex=t+%5Cin+%5B%5Calpha%2C+%5Cbeta%5D&bg=%23f6f5ed&fg=222222&s=0&c=20201002) . Is this also a directed set ?
. Is this also a directed set ?
Answer 3b: We need to choose two arbitrary elements say  and
and 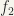 of the given set of continuous functions on
of the given set of continuous functions on ![[\alpha, \beta]](https://s0.wp.com/latex.php?latex=%5B%5Calpha%2C+%5Cbeta%5D&bg=%23f6f5ed&fg=222222&s=0&c=20201002) . Our desired “element” could be
. Our desired “element” could be 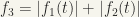 again defined on
again defined on ![[\alpha, \beta]](https://s0.wp.com/latex.php?latex=%5B%5Calpha%2C+%5Cbeta%5D&bg=%23f6f5ed&fg=222222&s=0&c=20201002) . Then, the given set becomes a directed set.
. Then, the given set becomes a directed set.
Note that the function 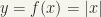 is continuous at zero also (but not differentiable at zero).
is continuous at zero also (but not differentiable at zero).
Question 3c:
Set inclusion.
Answer 3: Clearly, given any two arbitrary subsets, both are contained always in the given big set M or X. So, this is again a directed set.
Question 3d: The set of all integers greater than 1 is partially ordered if  means that “b is divisble by a.”
means that “b is divisble by a.”
Answer 3: So let us consider two arbitrary positive integers, both greater than 1, call them a and b. We want to know if there exist a positive integer, also greater than 1, call it c such that  and
and  ? That is, “c is divisible by a” and “c is divisible by b”. Clearly, c can be least common multiple of a and b. So, yes, this is also a directed set.
? That is, “c is divisible by a” and “c is divisible by b”. Clearly, c can be least common multiple of a and b. So, yes, this is also a directed set.
Problem 4:
By the greatest lower bound of two elements a and b of a partially ordered set M, we mean an element  such that
such that 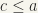 and
and  and there is no element
and there is no element  such that
such that 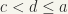 ,
, 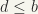 . Similarly, by the least upper bound of a and b, we mean an element
. Similarly, by the least upper bound of a and b, we mean an element  such that
such that  ,
,  , and there is no element
, and there is no element  such that
such that 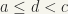 and
and  . By a lattice is meant a partially ordered set any two elements of which have both a greatest lower bound and a least upper bound. Prove that the set of all subsets of a given set M, partially ordered by set inclusion, is a lattice. What is the set theoretic meaning of the greatest lower bound and least upper bound of two elements of this set ?
. By a lattice is meant a partially ordered set any two elements of which have both a greatest lower bound and a least upper bound. Prove that the set of all subsets of a given set M, partially ordered by set inclusion, is a lattice. What is the set theoretic meaning of the greatest lower bound and least upper bound of two elements of this set ?
Solution 4:
It can be easily checked that the null set is the greatest lower bound and the set M itself if the least upper bound. (PS: these are the minimal and maximal elements of this set M respectively.)
Problem 5:
Prove that an order-preserving mapping of one ordered set onto another is automatically an isomorphism.
Solution 5:
By definition.
Problem 6:
Prove that ordered sums and products of ordered sets are associative, that is, prove that if 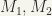 and
and  are ordered sets, then
are ordered sets, then
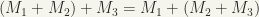
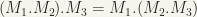
PS: comment: this allows us to drop the parentheses in writing ordered sums and products.
where the operations are as defined below:
Let 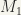 and
and  be two ordered sets of type
be two ordered sets of type  and
and 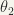 respectively. Then, we can introduce an ordering in the union
respectively. Then, we can introduce an ordering in the union 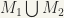 of the two sets by assuming that: (i) a and b have the same ordering as in
of the two sets by assuming that: (i) a and b have the same ordering as in 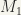 if
if  (ii) a and b have the same orderiing as in
(ii) a and b have the same orderiing as in  if
if  (iii)
(iii)  if
if  and
and  .
.
In this case/example, the ordered sum or union of three ordered sets 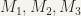 would mean that any two elements a, b would have the same ordering if
would mean that any two elements a, b would have the same ordering if  , or
, or  or
or  . Also, comparing with ordered sum of two ordered sets, we can say that
. Also, comparing with ordered sum of two ordered sets, we can say that  if and only if
if and only if  or
or  , or
, or  . In such a case, the ordered sum is also associative.
. In such a case, the ordered sum is also associative.
The operation of ordered product of two ordered sets is defined as follows: 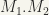 is the set of all pairs
is the set of all pairs  where
where  and
and  ordered in such a way that (i)
ordered in such a way that (i)  if
if 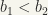 for arbitrary
for arbitrary 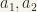 , and (ii)
, and (ii) 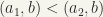 if
if  .
.
So, if we have three ordered sets 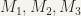 , we can define their ordered product
, we can define their ordered product  as consisting of all ordered triples such that (i)
as consisting of all ordered triples such that (i) 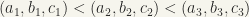 if and only if
if and only if  and
and 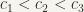 for arbitrary
for arbitrary  , and (ii)
, and (ii)  if
if  ;
; 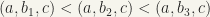 if
if  ;
; 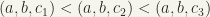 of
of 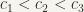 . In such a case, the product is well-defined and is also associative. (any comments ??)
. In such a case, the product is well-defined and is also associative. (any comments ??)
Problem 7:
Construct well-ordered sets with ordinals
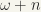 ,
,  ,
, 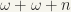 ,
, 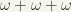 ,
, 
Show that the sets are all countable.
Solution 7:
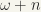 :
:  . This is countable because there can be bijection from the set
. This is countable because there can be bijection from the set 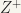 to the given set:
to the given set:  ,
, 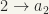 ,
,  ,
, 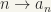 ,
,  ,
, 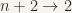 ,
, 
 :
: 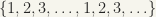 , this is also countable as it can be put in one-to-one correspondence with
, this is also countable as it can be put in one-to-one correspondence with 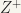 .
.
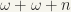 ;
;  . This is also countable in the same manner as the first example.
. This is also countable in the same manner as the first example.
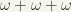 :
:  : this can be put in one-to-one correspondence with
: this can be put in one-to-one correspondence with 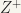
Problem 8:
Construct well-ordered sets with ordinals
 ,
, 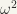 ,
, 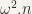 ,
, 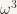 ,
,  .
.
Show that the sets are all countable.
Solution 8:
First let us recall the definition: An ordered set M is said to be well-ordered if every non empty subset A of M has a smallest (or, first) element, that is, an element 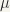 such that
such that  for every
for every 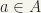 .
.
Ans 1:  is set :
is set : 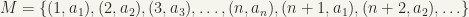 . This set is ordered clearly by the definition of ordered product of two ordered sets; and this is well-ordered if we define the first element to be
. This set is ordered clearly by the definition of ordered product of two ordered sets; and this is well-ordered if we define the first element to be  .
.
Ans 2:  : this set can be constructed as
: this set can be constructed as 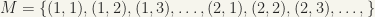 and we can define the first element as
and we can define the first element as  so that it becomes well-ordered under the usual definition of product of two ordered sets.
so that it becomes well-ordered under the usual definition of product of two ordered sets.
Ans 3:  : this set can be constructed as follows as an ordered product of three ordered sets:
: this set can be constructed as follows as an ordered product of three ordered sets:  . We see that this is also well-ordered if we define the first element to be
. We see that this is also well-ordered if we define the first element to be 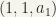 and “order or list or count” them as shown. (any comments ? )
and “order or list or count” them as shown. (any comments ? )
Ans 4:  : this can be well-ordered as above with clearly the first element to be
: this can be well-ordered as above with clearly the first element to be  . (any comments?)
. (any comments?)
PS: the explicit listing shows that all the above sets are clearly countable.
More later,
Cheers,
Nalin Pithwa
Mathematics Hothouse shares:
of a uniformly convergent sequence of functions
continuous on
is itself a function continuous on
.
where
.
to make the second term small for t sufficiently close to
.
figuring in the theorem 2 consists of a single point. Theorem 2 is recalled here: Nested sphere theorem: A metric space R is complete if and only if nested sequence
of closed spheres in R such that
as
has a non empty intersection
.
and let
. This is a metric space which we denote by m.
be a sequence of closed sets of R nested in the sense that
.
is non empty.
is finite. Prove that the union of a finite number of bounded sets is bounded.
of closed subsets of R such that
.
is an incomplete metric space.
establishes a homeomorphism between the whole real line
and the open interval
.
is the space of all real numbers, both equipped with the distance
. In this way, we can “construct the real number system.” However, there still remains the problem of suitably defining sums and products of real numbers and verifying that the usual axioms of arithmetic are satisfied.
and
are Cauchy sequences of rational numbers serving as “representatives” of real numbers
and
respectively, define
as the real number with representative
.