Month: October 2022

Princple of contradiction and principle of the excluded middle

Posted on by Nalin Pithwa

If X is a well-defined set in a universal set U,

then X \bigcap X^{'}=\phi this is called principle of contradiction.

That is, x cannot be both a member of X and not a member of X.

Principle of the excluded middle — X \bigcup X^{'}=U, that is an element x is either a member of set X or not a member of set X.

Cheers,

Nalin Pithwa

Kinds of Definition (by Linus Pauling)

Posted on by Nalin Pithwa

Definitions may be either precise or imprecise. The mathematician may define the words that he uses precisely; in his further discussion he then adheres rigorously to the defined meaning of each word. (But for example, the definition of function, the definition of metric space, the definition of topology etc. did take substantial time to evolve…once agreed upon all mathematical community adheres to the definition and hence, math is an exact science in that sense !) We also have standard definitions of fundamental physical quantities, example one kilogram. One kilogram is the mass of as standard object (as defined in SI system of units), the prototype kilogram that is kept in Paris. Similarly, the gram is defined rigorously and precisely as 1/1000 the mass of the kilogram.

On the other hand, the words that are used in describing nature, which is itself quite complex/complicated, may not be capable of precise definition. In giving a definition for such a word the effort is made to describe the “accepted usage.”

Cheers,

Nalin Pithwa

Words of advice, preliminaries from H L Royden: logic and methods of proof

Posted on by Nalin Pithwa

Reference: Real Analysis Third Edition by H L Royden, Prentice Hall of India, avallable Amazon India.

(Extracted from Prologue to the student)

Statements and their proofs:

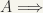Most of the principal statements (theorems, propositions, etc.) in mathematics have the standard form “if A, then B” or in symbols A \Longrightarrow B. The contrapositive of A \Longrightarrow is the statement (\neg A) \Longrightarrow (\neg B). It is readily seen that a statement and its contrapositive are equivalent; that is, if one is true, then so is the other. The direct method of proving a theorem of the form A \Longrightarrow B is to start with A, deduce various consequences from it,, and end with B. 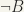It is some times easier to prove a theorem by contraposition; that is, by starting with \neg B and deriving \neg A. A third method of proof is proof by contradiction or reductio ad absurdum. 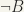We begin with A and \neg B and derive a contradiction. All students are enjoined in the strongest possible terms to eschew proofs by contradiction ! There are two reasons for this prohibition; First, such proofs are very often fallacious, the contradiction on the final page arising from an erroneous deduction on an earlier page, rather than from the incompatibility of A with 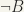\neg B. Second, even when correct, such a proof gives little insight into the connection between A and B, whereas both the direct proof and the proof by contraposition construct a chain of argument connecting A with B. One reason that mistakes are so much more likely in proofs by contradiction than in direct proofs or proofs by contraposition is that in a direct proof (assuming the hypothesis is not always false) all deductions from the hypothesis are true in those cases where the hypothesis holds, and similarly for proofs by contraposition (if the conclusion is not always true) the deductions from the negation of the conclusion are true in those cases where the conclusion is false. Either way, one is dealing with true statements, and one’s intuition and knowledge about what is true help to keep one from making erroneous statements. In proofs by contradiction, however, you are (assuming the theorem true) in the unreal world where any statement can be derived, and so the falsity of a statement is no indication of an erroneous deduction.

PS: A theorem is a statement of such importance that it should be remembered since it is used frequently. A proposition is a statement of interest in its own right but which has less frequent application. A lemma is usually used only for proving propositions and theorems in the same “section.” A lemma is a little useful result on the way to proving “bigger” things !

Logical notation:

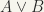It is convenient to use some abbreviations for logical expressions. We use “&” to mean “and” so that “A & B” means “A and B”;\vee means “or” so that “A \vee B” means “A or B or both” ; \neg means “not” or “it is not the case that”, so that “\neg A” means “it is not the case that A”. Another important notation is the one that we express by the symbol “\Longrightarrow“. It has a number of synonyms in English, so that the statement “A \Longrightarrow B” can be expressed by saying “If A, then B”, “A implies B”, “A only if B”,, “A is sufficient for B” or “B is necessary for A.” The statement A \Longrightarrow B is equivalent to each of the statements “(\neg A) \vee B” and \neg(A \& (\neg B)). We also use the notation A \Longleftrightarrow B to mean (A \Longrightarrow B) \& (B \Longrightarrow A). The English synonyms for A \Longleftrightarrow B are “A if and only if B”, “A is equivalent to B”, and “A is necessary and sufficient for B”.

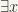In addition to the preceding symbols we use two further abbreviations: “(x)” or “\forall x” to mean “for all x” or “for every x”, and \exists x to mean “there is an x” or “for some x”. Thus, the statement 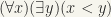(\forall x)(\exists y)(x < y) says that for every x there is a y larger than x. Similarly, (\exists y)(\forall x)(x < y) says that there is a y which is larger than every x. Note that these two statements are different: as applied to real numbers, the first is true and the second is false.

Since saying that there is an x such that A(x) means that it is not the case that for every x we have \neg A(x), we see that “(\exists x)A(x) \Longleftrightarrow \neg (x) \neg A(x)“. Similarly, (x)A(x) \Longleftrightarrow \neg(\exists x)\neg A(x). This rule is often convenient when we wish to express the negative of a complex statement. Thus,

\neg\{ (x)(\exists y)(x < y)\} \Longleftrightarrow \neg(x) \neg(y) \neg(x <y) \Longleftrightarrow (\exists x)(y) \neg (x < y) (\exists x)(y)(y \leq x) where we have used the properties of the real numbers to infer that \neg(x < y) \Longleftrightarrow (y \leq x).

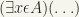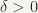We sometimes modify the standard logical notation slightly and write (\epsilon >0)(\ldots), (\exists \delta >0)(\ldots) and (\exists x \epsilon A)(\ldots) to mean “for every \epsilon greater than 0 (\ldots)“, “there is a \delta>0 greater than 0 such that (\ldots)” and “there is an x in the set A such that (\ldots)“. This modification shortens our expressions. 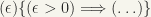For example, (\epsilon>0)(\ldots) would be written in standard notation (\epsilon)\{ (\epsilon>0) \Longrightarrow (\ldots)\}.

For a thorough discussion of the formal use of logical symbolism, we need to refer to Patrick Suppes, Axiomatic Set Theory, Dover Publications Inc., (available Amazon India).

Cheers,

Nalin Pithwa

A problem on Euclidean topology and its solution

Posted on by Nalin Pithwa

Reference: Chapter 1, Topology by Hocking and Young, Dover Publications Inc.

Question: Exercises 1-6: In E^{n}, let x = (x_{1}, x_{2}, x_{3}, \ldots, x_{n}) and y=(y_{1}, y_{2}, y_{3}, \ldots, y_{n}), and define d^{'}(x,y) = \Sigma_{i=1}^{n}|x_{i}-y_{i}| and d^{''}(x,y) = \max_{i}|x_{i}-y_{i}|. Show that both d^{'} and d^{''} give the same topology as the Euclidean metric. What do the elements look like ?

Solution:

Consider first the simpler case of E^{2}.

Let x=(x_{1},x_{2}) and y-(y_{1}, y_{2}).

Then, d^{'}(x,y)= \Sigma_{i=1}^{2}|x_{i}-y_{i}|=|x_{1}-y_{1}|+|x_{2}-y_{2}|<R, say

In the Euclidean metric, d(x,y) = \sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}<R, also. Then, squaring both sides results in the following: (x_{1}-y_{1})^{2}+(x_{2}-y_{2})^{2}<R^{2}.

Now, squaring both sides of d^{'} inequality gives us: |x_{1}-y_{1}|^{2}+|x_{2}-y_{2}|^{2} + 2|x_{1}-y_{1}| \times |x_{2}-y_{2}|<R^{2} that is, on further manipulation, we get

|x_{1}-y_{1}|^{2}+|x_{2}-y_{2}|^{2} <R^{2} - 2|x_{1}-x_{2}| \times |y_{1}-y_{2}| < R^{2} resulting in the same inequality as Euclidean topology.

The general case of E^{n} is similar. The topology d^{'} is interior of all rectangles.

Now, consider d^{''} in E^{2}. We have d^{''}(x,y) = \max_{i}|x_{i}-y_{i}| which is clearly less than R if R is also the radius of the Euclidean open ball. The d^{''} topology is also interior of rectangles. The general case is similar.

QED.

Cheers,

Nalin Pithwa