Reference: A Course on Topological Groups by K Chandrashekharan, Hindustan Book Agency, available Amazon Indiia.
Chapter 1. Topological Preliminaries:
Section 1.1 Topological Space:
A topology T in a set X is a class of subsets of X (called open sets) satisfying the following axioms:
(1) the union of any number of open sets is open
(2) the intersection of any two (or finitely many) open sets is open
(3) X and the emtpy set of null set  are both open.
are both open.
A topological space is a set X with a topology T in X. T is called the trivial topology if 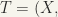 latex \phi$) and is called the discrete topology if T= (A:
latex \phi$) and is called the discrete topology if T= (A:  ). (PS: the trivial topology has too many limit points; it is like a lumped mass) whereas the discrete topology has no limit points, yet this latter topology is quite useful ! )
). (PS: the trivial topology has too many limit points; it is like a lumped mass) whereas the discrete topology has no limit points, yet this latter topology is quite useful ! )
Let X be a topological space and  . We define an induced topology in A as follows: the class of open sets in A is the class of sets of the form
. We define an induced topology in A as follows: the class of open sets in A is the class of sets of the form  where U runs through all open sets in X.
where U runs through all open sets in X.
In a topological space X, a closed set is any set whose complement is an open set.
The closure  of any set E is the intersection of all closed sets containing E. By axioms (1) and (3) above, the closure is a closed set.
of any set E is the intersection of all closed sets containing E. By axioms (1) and (3) above, the closure is a closed set.
A neighbourhood of  is any open set containing x. Let
is any open set containing x. Let 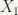 and
and  be two topological spaces and f a mapping
be two topological spaces and f a mapping

A mapping is an assignment to each 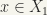 of an element f(x) in
of an element f(x) in  . Then f is continuous if and only if for every open set
. Then f is continuous if and only if for every open set  , the set
, the set  is an open set in
is an open set in  . Here,
. Here,  .
.
Let 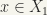 . We say that f is continuous at x, if to every neighbourhood U of f(x) there exists a neighbourhood V of x such that
. We say that f is continuous at x, if to every neighbourhood U of f(x) there exists a neighbourhood V of x such that 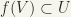 . We say that f is continuous, if f is continuous at every point of
. We say that f is continuous, if f is continuous at every point of 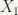 . This definition is equivalent to the preceding one.
. This definition is equivalent to the preceding one.
The mapping f is said to be open if for every open set 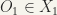 , the set
, the set  is an open set in
is an open set in  .
.
Let 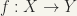 and
and  be two continuous mappings. Then the composite mapping
be two continuous mappings. Then the composite mapping  is continuous.
is continuous.
Examples
(i) If X is a discrete topological space, Y is a topological space, then every mapping 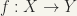 is continuous. (PS: this is vacuously true).
is continuous. (PS: this is vacuously true).
(ii) If X is any topological space, and Y a set wtih the trivial topology, then 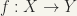 is continuous.
is continuous.
(iv) 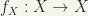 is the identity mapping.
is the identity mapping.
The topological product of two topological spaces 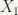 and
and  is the topological space
is the topological space 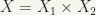 , whose set is the cartesian product of
, whose set is the cartesian product of 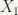 and
and  , namely,
, namely, 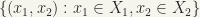 with the open sets being all unions of sets of the form
with the open sets being all unions of sets of the form 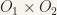 where
where  is an open set in
is an open set in 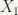 and
and 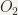 is an open set in
is an open set in  . Sets of the form
. Sets of the form 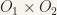 form a basis of open sets in
form a basis of open sets in 
Note that if 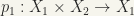 and
and  are the projections defined by
are the projections defined by  and
and  respectively then
respectively then 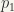 and
and  are continuous mappings where
are continuous mappings where  and
and 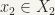 .
.
COVERING. A family  where
where  of subsets of a set X is a covering of X, if
of subsets of a set X is a covering of X, if 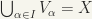 . That is to say, each point of X belongs to at least one
. That is to say, each point of X belongs to at least one 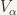 . If further, X is a topological space, and each
. If further, X is a topological space, and each 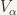 is an open subset of X, we say that
is an open subset of X, we say that 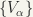 is an open covering of X.
is an open covering of X.
A covering  is a finite covering if I is a finite set.
is a finite covering if I is a finite set.
COMPACT SETS. A topological space X is said to be compact if every covering of X contains a finite subcover. That is to say,  where
where  is open implies that there exists
is open implies that there exists  all belonging to I such that
all belonging to I such that  . A subset
. A subset  is compact if A is compact in the induced topology.
is compact if A is compact in the induced topology.
Examples:
(i) The  is not compact.
is not compact.
(ii) Let X be a topological space and  / If A consists of finitely many elements of X, then A is compact. (PS: A finite point set has no limit points).
/ If A consists of finitely many elements of X, then A is compact. (PS: A finite point set has no limit points).
(iii) Let a, b belong to reals. Let  . Then the set
. Then the set  is compact.
is compact.
An equivalent definition of compactness is the following:
If  is a family of closed sets such that every finite subfamily has a non-empty intersection, then
is a family of closed sets such that every finite subfamily has a non-empty intersection, then 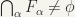 . (If
. (If  is a family of closed sets with the finite intersection property, then the intersection of the whole class is non-empty).
is a family of closed sets with the finite intersection property, then the intersection of the whole class is non-empty).
A closed subset of a compact set is compact. A continuous image of a compact set is compact. (If 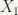 is compact,
is compact,  is Hausforff, and
is Hausforff, and  is continuous, then
is continuous, then  is closed in
is closed in  ).
).
A product of compact spaces is compact (Tychonoff theorem).
A space X is locally compact if for every  , there is a neighbourhood
, there is a neighbourhood  of x such that the closure of
of x such that the closure of  is compact.
is compact.
Every compact space is locally compact but not vice-versa.
HOMEOMORPHISMS.
Let X and Y be topological spaces and f a mapping 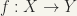 . We say that f is a homeomorphism if f is one-to-one, onto and both f and
. We say that f is a homeomorphism if f is one-to-one, onto and both f and  are continuous.
are continuous.
Two topological spaces X and Y are said to be homeomorphic if there exists a homeomorphism f from X to Y.
Examples:
(i)  and
and 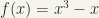 for
for  .
.
(ii) (a) 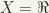 and
and  . X and Y are homeomorphic under the mapping
. X and Y are homeomorphic under the mapping 
(ii) (b)  and the open unit ball
and the open unit ball 
(iii) If 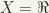 and
and  then X and Y are not homeomorphic. Note that Y is compact while
then X and Y are not homeomorphic. Note that Y is compact while  is not compact.
is not compact.
(iv) If a mapping is one to one, onto and continuous, it does not follow that it is a homeomorphism. For example, let X = a set with more than one element and T is the discrete topology in X, and 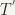 is the trivial topology in X. Then the identity mapping
is the trivial topology in X. Then the identity mapping 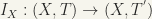 is continuous, but not a homeomorphism. (PS:
is continuous, but not a homeomorphism. (PS:  is not a bijection).
is not a bijection).
SEPARATION AXIOMS:
Two sets 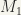 and
and  can be separated by open sets if there exist open sets
can be separated by open sets if there exist open sets  and
and 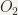 such that
such that  and
and  and
and 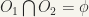 .
.
 and
and  can be separated by a real function if there exists a continuous real function f on X such that
can be separated by a real function if there exists a continuous real function f on X such that  for
for  and
and  for
for  and
and  for
for  .
.
 separation axiom:
separation axiom:
For any two disjoint points, there exists a neighbourhood of either point not containing the other. (This implies that the complement of each point is an open set or that each point is a closed set).
 separation axiom:
separation axiom:
Any two distinct points can be separated by open sets (or any two distinct points have disjoint neighbourhoods). A topological space is Hausdorff if it satisfies  ).
).
Examples:
(i) A set X with the discrete topology (PS: If a topological space is  , then it is also
, then it is also  but the converse is not true in general).
but the converse is not true in general).
(ii) If X is a set with more than one element, then X with the trivial topology is not Hausdorff !
(iii) If X is Hausdorff and  , then A is Hausdorff with the induced topology.
, then A is Hausdorff with the induced topology.
(iv) Let  be compact,
be compact,  be Hausdorff and
be Hausdorff and  be continuous. Then
be continuous. Then  is closed in
is closed in  .
.
(v) Let X be Hausdorff with  and let A be compact. Then A is closed.
and let A be compact. Then A is closed.
AXIOM  :
:
A closed set F and a point  can be separated by open sets.
can be separated by open sets.
A topological space is regular if it satisfies separation axioms  and
and  / A completely regular topological space is one in which a closed set F and a point
/ A completely regular topological space is one in which a closed set F and a point  can be separated by a real function.
can be separated by a real function.
AXIOM  :
:
Two disjoint closed sets can be separated by open sets. A topological space is normal if it satisfies seperation axioms  and
and  .
.

(Solomon Lefshetz, Algebraic Topology): In a normal space, every two disjoint closed sets can be separated by a real function.
Section 1.2 
A topological group is a set G which is both a group and a  space with the topology and group structure related by the assumption that the functions
space with the topology and group structure related by the assumption that the functions  and
and  are continuous. Here,
are continuous. Here,  and
and  is the group inverse element of x in G.
is the group inverse element of x in G.
Equivalently, the function  (from
(from 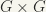 to G) is continuous.
to G) is continuous.
Examples:
(i) The additive group of real numbers is the underlying group of a topological group whose underlying topological space is the usual space of real numbers. More generally, the Euclidean n-space under the usual topology.
(ii) Any group with the usual discrete topology (every set is its own closure).
(iii) The n-dimensional torus (that is to say, the product of n circles). Here a circle is the topological group  under multiplication.
under multiplication.
(iv)  , the general linear group, that is, the group of all non-singular
, the general linear group, that is, the group of all non-singular  matrices with complex coefficients. For the topology use that “induced” by considering the
matrices with complex coefficients. For the topology use that “induced” by considering the  matrices as a subset of
matrices as a subset of  .
.
(v) Any product of topological groups.
Let e be the identity in the topological group G. If  then
then  (this is the definition, by the way)
(this is the definition, by the way)
(1) If  , and O is a neighbourhood of x, there exist neighbourhoods P of x and Q of y such that
, and O is a neighbourhood of x, there exist neighbourhoods P of x and Q of y such that 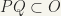 .
.
Let  denote the mapping
denote the mapping  and
and  . Since
. Since  is continuous and O is open, it follows that
is continuous and O is open, it follows that  is open. Now
is open. Now  contains
contains  so it also contains a set of the form
so it also contains a set of the form 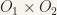 where
where  is a neighbourhood of x, and
is a neighbourhood of x, and 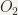 is a neighbourhood of y, and
is a neighbourhood of y, and  . Take
. Take  and
and  .
.
(1′) If 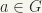 , then for every neighbourhood V of
, then for every neighbourhood V of  there exists a neighbourhood U of a, such that
there exists a neighbourhood U of a, such that 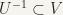 . This follows again from the fact that
. This follows again from the fact that  is continuous. (If g is a continuous mapping of a topological space R into
is continuous. (If g is a continuous mapping of a topological space R into 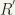 , then for every point
, then for every point 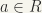 and every neighbourhood
and every neighbourhood  of
of 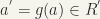 there exists a neighbourhood U of a such that
there exists a neighbourhood U of a such that 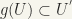 )
)
(2) For each  , the mappings
, the mappings  and
and  are homeomorphisms or topological mappings.
are homeomorphisms or topological mappings.
The mapping 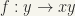 is one-to-one (because
is one-to-one (because  implies that
implies that  ). The inverse mapping
). The inverse mapping  is of the same form. Hence, it suffices to prove that f is continuous. Let O be any neighbourhood of xy. By (1) there exists a neighbourhood
is of the same form. Hence, it suffices to prove that f is continuous. Let O be any neighbourhood of xy. By (1) there exists a neighbourhood  of x, and a neighbourhood
of x, and a neighbourhood 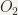 of y such that
of y such that 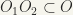 . Hence,
. Hence,  , that is to say
, that is to say  . This shows that f is continuous (cf. (1′)).
. This shows that f is continuous (cf. (1′)).
(3) The mapping  is a homeomorphism. For
is a homeomorphism. For  is one-to-one, and is its own inverse (by group law). It is continuous by definition.
is one-to-one, and is its own inverse (by group law). It is continuous by definition.
(4) If O is open in G, then  are also open, where
are also open, where  and
and 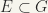 .
.
By (2) xO and Ox are open so is  by (3). Now EO is equal to
by (3). Now EO is equal to 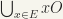 , hence, open, similarly also OE.
, hence, open, similarly also OE.
(5) If V is any neighbourhood of e, it contains a neighbourhood W of e, such that  .
.
Proof:
Since  , there exist neighbourhoods
, there exist neighbourhoods  of e, and
of e, and  of
of  , such that
, such that  by (1).
by (1).
Let 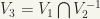 . Then
. Then  is open and
is open and 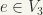 so that
so that  is a neighbourhood of e.
is a neighbourhood of e.
Next  . For
. For  implies
implies 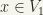 and
and  , and
, and 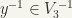 implies that
implies that 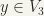 , which in turn implies that
, which in turn implies that 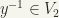 . Hence,
. Hence, 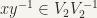 implies that
implies that  . Choose
. Choose  .
.
(6) A neighbourhood V of e is defined to be symmetric if and only if 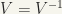 .
.
Every neighbourhood W of e contains a symmetric neighbourhood (for example,  ). By (4)
). By (4) 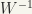 is open. Hence,
is open. Hence,  is a symmetric neighbourhood of e.
is a symmetric neighbourhood of e.
(7) Every neighbourhood of  is of the form xV as well as of the form Wx, where V and W are neighbourhoods of the identity.
is of the form xV as well as of the form Wx, where V and W are neighbourhoods of the identity.
Let U be any neighbourhood of x. Then, 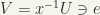 , and
, and  is open by (4). Hence, V is a neighbourhood of e. Similarly,
is open by (4). Hence, V is a neighbourhood of e. Similarly,  is a neighbourhood of e. Hence,
is a neighbourhood of e. Hence,  .
.
(8) The continuity of  is equivalent to the continuity of
is equivalent to the continuity of  together with the continuity of
together with the continuity of  .
.
(i) If  and
and  are continuous, then
are continuous, then  and
and  are continuous, hence the composite
are continuous, hence the composite  is continuous.
is continuous.
(ii) Conversely, if  is continuous, then
is continuous, then  is continuous. Further,
is continuous. Further,  is continuous (obviously). Hence,
is continuous (obviously). Hence,  is continuous. Therefore,
is continuous. Therefore,  is continuous. But by hypothesis,
is continuous. But by hypothesis,  is continuous. Hence,
is continuous. Hence,  is continuous.
is continuous.
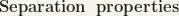

The topological space of a topological group G is Hausdorff.

Let x,y belong to a group G such that x and y are distinct elements. By the  property (Given two points of S, each of them lies in an open set not containing the other) we can find a neighbourhood V of e not containing
property (Given two points of S, each of them lies in an open set not containing the other) we can find a neighbourhood V of e not containing  . By (5) there exists a neighbourhood
. By (5) there exists a neighbourhood  of e, such that
of e, such that  . Then
. Then 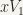 ,
, 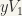 are neighbourhoods of x and of y respectively. And
are neighbourhoods of x and of y respectively. And 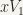 ,
, 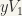 are neighbourhoods of x and of y respectively. And we claim that
are neighbourhoods of x and of y respectively. And we claim that 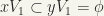 . This is because of the following: (indirect proof) if
. This is because of the following: (indirect proof) if  then there exist points (or elements of G or T)
then there exist points (or elements of G or T) 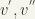 such that
such that  so that
so that  contradicting the choice of V. Hence, the Hausdorff axiom is satisfied because
contradicting the choice of V. Hence, the Hausdorff axiom is satisfied because  .
.

If 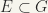 , then
, then  where V extends over all neighbourhoods of e. (Note that E could be any, some or run through all subsets of G)
where V extends over all neighbourhoods of e. (Note that E could be any, some or run through all subsets of G)
First we prove that (i) 
If any arbitrary element  for all V. we shall see/prove that every neighbourhood of x intersects E and so we would have
for all V. we shall see/prove that every neighbourhood of x intersects E and so we would have 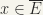 .
.
Now, let 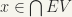 and let O be any neighbourhood of x. Then by (7) above,
and let O be any neighbourhood of x. Then by (7) above,  , where V is a neighbourhood of e. By hypothesis,
, where V is a neighbourhood of e. By hypothesis,  , which implies that
, which implies that 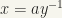 , where
, where  ,
,  , or
, or 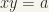 . Hence xV intersects E (that is, has a non-empty intersection with E). Therefore, O intersects E, hence,
. Hence xV intersects E (that is, has a non-empty intersection with E). Therefore, O intersects E, hence,  .
.
(ii)  .
.
If  , then every neighbourhood of x intersects E. By (7),
, then every neighbourhood of x intersects E. By (7),  is a neighbourhood of x (where V is a neighbourhood of e). Hence,
is a neighbourhood of x (where V is a neighbourhood of e). Hence,  intersects E. This implies that
intersects E. This implies that  (for there exists y
(for there exists y 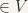 , such that
, such that  , or
, or 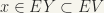 . Hence,
. Hence, 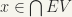
 A topological group is homogeneous. Given any two elements —-
A topological group is homogeneous. Given any two elements —- 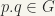 , there exists a topological mapping f of G onto itself which takes p into q.
, there exists a topological mapping f of G onto itself which takes p into q.
Take  and take
and take 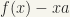 .
.
It is sufficient for many purposes therefore to verify local properties for a single element only. For example, to show that G is locally compact, it is suffieient to show that its identity e has a neighbourhood U whose closure is compact — so also with regularity.
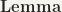
The topological space of a topological group G is regular (Kolmogorov).
Note: A topological space is  if the following is true: Given two points of a topological space S, each of them is contained in an open set not containing the other. Axiom
if the following is true: Given two points of a topological space S, each of them is contained in an open set not containing the other. Axiom  : If C is a closed set in the space S, and if p is a point not contained in C, then there are disjoint open sets in S, one containing C and the other containing p.3
: If C is a closed set in the space S, and if p is a point not contained in C, then there are disjoint open sets in S, one containing C and the other containing p.3
A space that satisfies both  and
and  is called regular.
is called regular.

We can separate e and any closed set F not containing not containing e. Now let  . Then O is a neighbourhood of e. Now there exists a neighbourhood V of e, such that
. Then O is a neighbourhood of e. Now there exists a neighbourhood V of e, such that 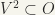 (because of (5) and (6) above). (Remark I think the author has assumed here that V is symmetric)V and
(because of (5) and (6) above). (Remark I think the author has assumed here that V is symmetric)V and  are disjoint open sets. We shall see that
are disjoint open sets. We shall see that  .
.
Since V is a neighbourhood of e, that will prove this lemma. Now,
 , where W is a neighbourhood of e (by Lemma 2)
, where W is a neighbourhood of e (by Lemma 2)
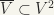 (since V is a W, a neighbourhood of e_
(since V is a W, a neighbourhood of e_
 (by the choice of V and O).
(by the choice of V and O).
(So  (by definition of O)
(by definition of O)
Hence,  or
or  or
or 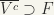 .
.
 Atopological space which is the underlying space of a topological group G is completely regular.
Atopological space which is the underlying space of a topological group G is completely regular.
 It is sufficient to show that if F is a closed set not containing e, then F and e can be separated by a continuous real function. (cf. the remark above)
It is sufficient to show that if F is a closed set not containing e, then F and e can be separated by a continuous real function. (cf. the remark above)
Note: Definition: A topological spacce is said to be  (also called
(also called
 ) if for every point p of S and for any open set U containing p, there is a continuous function of S to
) if for every point p of S and for any open set U containing p, there is a continuous function of S to 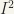 such that
such that  and
and 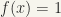 for all points x in
for all points x in  . I is a closed interval
. I is a closed interval ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=%23f6f5ed&fg=222222&s=0&c=20201002) .
.
Let  . Then V is a neighbourhood of e. Choose a sequence
. Then V is a neighbourhood of e. Choose a sequence  of neighbourhoods of e, such that
of neighbourhoods of e, such that  ,
,  where
where  . [This is possible, see the proof of Lemma 3 in which (5) and (6) were used.
. [This is possible, see the proof of Lemma 3 in which (5) and (6) were used.
Let  be finite dyadic real number (a dyadic rational or binary rational number is a number that can be expressed as a fraction with denominator whose fraction is a power of two)
be finite dyadic real number (a dyadic rational or binary rational number is a number that can be expressed as a fraction with denominator whose fraction is a power of two)
 where
where 
Define  (group product ) where
(group product ) where  is e.
is e.
We will show that 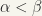 implies that
implies that 
If 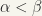 then first j digits agree for some
then first j digits agree for some  so that
so that

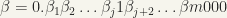
and  for some
for some 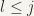
Now define
 note that here
note that here  is the right most 1.
is the right most 1.
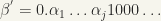
Then

Clearly, 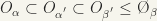 (since
(since 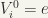
We shall see that
 (which will imply that
(which will imply that 
Let 
Then
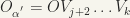 and
and 
Hence by Lemma 2,
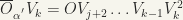
 (since
(since  )
) by definition
by definition
Hence,  and therefore
and therefore 
Now detine
 if
if 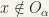
 if x is in some
if x is in some 
Then we have  for all
for all  . Furtheer
. Furtheer
 for x = e (since Slatex V_{i}^{0}=e$)
for x = e (since Slatex V_{i}^{0}=e$)
 for
for 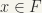 (for
(for  ) (as `
) (as ` (see above)
(see above)
We shall see that f is continuous. The sets  and
and  , (where k is a real number) are both open. For,
, (where k is a real number) are both open. For,
 This is equal to the following:
This is equal to the following: 
 So we get the following now:
So we get the following now:
 (this is a closed set)
(this is a closed set)
Note that  hence
hence

for if x is such that  , and
, and  such that
such that  , then
, then 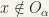 for all
for all 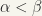 (since
(since  ), hence
), hence  , a contradiction. The opposite inclusion is trivial. Thus,
, a contradiction. The opposite inclusion is trivial. Thus,

But  since on the one hand,
since on the one hand, 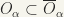 and on the other
and on the other  so that
so that  implies that
implies that 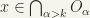 (as
(as  is a dyadic rational), hence
is a dyadic rational), hence  is open.
is open.
Similarly,  is also open. For if the set contains the point x, it contains a whole neighbourhood of it; for, if x is such that
is also open. For if the set contains the point x, it contains a whole neighbourhood of it; for, if x is such that 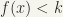 , then there exists
, then there exists 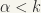 , such that
, such that  , which is neighbourhood of x all of which is contained in
, which is neighbourhood of x all of which is contained in 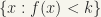 note (
note ( )
)
Similarly,  is also open. For if the set contains the point x, it contains a whole neighbourhood of it; for, if x is such that
is also open. For if the set contains the point x, it contains a whole neighbourhood of it; for, if x is such that 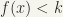 , then there exists
, then there exists  such that
such that  which is a neighbourhood of x all of which is contained in
which is a neighbourhood of x all of which is contained in  ,
, 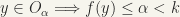 .
.
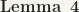
If  are compact subsets of G, then
are compact subsets of G, then  is compact
is compact
Proof: Consider the mapping  which takes
which takes  into xy. This is continuous. The product
into xy. This is continuous. The product  is compact (Tychonoff). The proof follows from the fact that the continuous image of a compact set is compact.
is compact (Tychonoff). The proof follows from the fact that the continuous image of a compact set is compact.

If 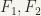 are closed, it does not follow that
are closed, it does not follow that  is closed. In
is closed. In  let
let  and
and  . Then
. Then  . Here by Q we mean the set of rational numbers greater than or equal to zero.
. Here by Q we mean the set of rational numbers greater than or equal to zero.

A locally compact group is normal.
Note: we recall here the definition of normal: Axiom  : Given two points of a topological space S, each of them lies in an open set not containing the other. Axiom
: Given two points of a topological space S, each of them lies in an open set not containing the other. Axiom  : If H and K are disjoint closed sets in the topological space S, then there exist disjoint open sets, one containing H and the other containing K. A
: If H and K are disjoint closed sets in the topological space S, then there exist disjoint open sets, one containing H and the other containing K. A  space or a normal space is one that satisfies both Axiom
space or a normal space is one that satisfies both Axiom  and Axiom
and Axiom  .
.
If the group is compact, the proof is easy since compactness together with regularity (or Hausdorff ) implies normality.
Otherwise take a symmetric neighbourhood U of e with compact closure, and consider  . Then
. Then 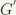 is an open and closed subgroup of G, and it is sufficient to prove normality for
is an open and closed subgroup of G, and it is sufficient to prove normality for 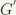 . To do that, use the fact that
. To do that, use the fact that 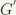 is
is 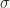 compact. That is,
compact. That is,  where
where 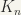 is compact.
is compact.  .
.
Note: A locally compact  group is para-compact, hence normal. (Reference: Hewitt and Ross, Abstract Harmonic Analysis. Volume I. page 76, Theorem 8.13
group is para-compact, hence normal. (Reference: Hewitt and Ross, Abstract Harmonic Analysis. Volume I. page 76, Theorem 8.13


Let G be a topological group, and H a subset of G. Then H is, by definition, a subgroup of the topological group G if and only if H is a subgroup of the abstract group G, and H is a closed set in the topological space G.
Let G be a topological group, and H a subset of it which is a subgroup of G considered as an abstract group. Then H is also a topological subgroup with the induced topology. In particular, a subgroup of an abstract group which is a topological group is itself a topological group.
A subgroup N of the topological group G is defined to be a normal subgroup if N is the normal subgroup of the abstract group G.
Let G be a topological group, and let H be a subgroup of the abstract group G. Then  is a subgroup of the topological group G. If H is a normal subgroup of the abstract group G, then
is a subgroup of the topological group G. If H is a normal subgroup of the abstract group G, then  is also normal, that is, a normal subgroup of the topological group G.
is also normal, that is, a normal subgroup of the topological group G.
Let us recall that if G is any group, and H a subgroup of G, a left coset of H is a subset of G of the form xH, where x is an element of G. The left coset set is the set of all left cosets of H, denoted by G/H. We have a natural map or projection 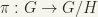 where
where 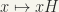 defined by
defined by  equal to the left coset of H which contains x.
equal to the left coset of H which contains x.
If G is a topological group, we shall topologize G/H, assuming that H is closed. A set  is open if and only if
is open if and only if 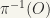 is open in G. This means that we require
is open in G. This means that we require  to be a continuous map.
to be a continuous map.
 G/H is a
G/H is a  space, and
space, and  is open.
is open.
Again we first recall definitions of  and open: Axiom
and open: Axiom  says: Given two points of a topological space S, each of them lies in an open set not containing the other. Also, a mapping f is said to be open if for every open set
says: Given two points of a topological space S, each of them lies in an open set not containing the other. Also, a mapping f is said to be open if for every open set  in
in 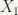 the set $latex $f(O_{1}) is an open set in
the set $latex $f(O_{1}) is an open set in  .. Note:
.. Note:  .
.

Since H is closed, xH is also closed. (homeomorphism) so that 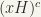 is open in G. Write
is open in G. Write  , coset containing x. Now
, coset containing x. Now  , which is open. Therefore, G/H is
, which is open. Therefore, G/H is  (the complement of each point is an open set). We know that
(the complement of each point is an open set). We know that  is continuous, we have to show that it is also open. Let O be open, where
is continuous, we have to show that it is also open. Let O be open, where 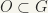 . Then
. Then  is in the coset space; it is open if and only if
is in the coset space; it is open if and only if  is open. But
is open. But  is OH, which is open since
is OH, which is open since  , where Ox is open. Thus, O open
, where Ox is open. Thus, O open  is also open. QED.
is also open. QED.
 G/H is a
G/H is a 
Let us recall definition of  or Hausdorff space: Given two distinct points of a topological space S, there are disjoint open sets each containing just one of the two points.
or Hausdorff space: Given two distinct points of a topological space S, there are disjoint open sets each containing just one of the two points.

Let  and
and  be two distinct points of
be two distinct points of  and
and 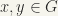 such that
such that 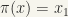 and
and 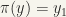 . Choose a neighbourhood v of e such that
. Choose a neighbourhood v of e such that 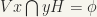 . This is possible because
. This is possible because 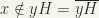 (H is closed as yH is closed. Vx is a neighbourhood of x, use the definition of
(H is closed as yH is closed. Vx is a neighbourhood of x, use the definition of  .) It follows that
.) It follows that 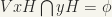 . For if
. For if  , then
, then 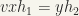 , say,, where
, say,, where 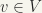 ,
, 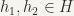 . Hence
. Hence  , which contradicts
, which contradicts 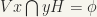 .
.
Let  be a neighbourhood of e such that
be a neighbourhood of e such that  . Then
. Then  , hence
, hence  . Therefore,
. Therefore,
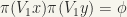
Now  since
since  and
and 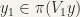 and
and  ,
,  are open (by Lemma 1,
are open (by Lemma 1, 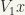 and
and  are open, and by Lemma 5
are open, and by Lemma 5  is open mapping. Hence,
is open mapping. Hence,  are separated by disjoint open sets. QED.
are separated by disjoint open sets. QED.

If G is any topological group, H a closed subgroup, we have topologized the coset set G/H in such a way that it is a  space. We may call G/H the quotient space, and the given topology the quotient space topology. On the other hand, if G is any group, and H a normal subgroup (that is,
space. We may call G/H the quotient space, and the given topology the quotient space topology. On the other hand, if G is any group, and H a normal subgroup (that is,  ,
, 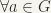 ,
, 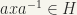 or
or  ), then the coset G/H is, in fact, a group known as the quotient group. The next lemma shows that the quotient group, with the quotient space topology is a topological group, if, to start with, G is a topological group.
), then the coset G/H is, in fact, a group known as the quotient group. The next lemma shows that the quotient group, with the quotient space topology is a topological group, if, to start with, G is a topological group.
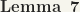 If G is a topological group, and H a normal subgroup, then the quotient group G/H with the quotient space topology is a topological group.
If G is a topological group, and H a normal subgroup, then the quotient group G/H with the quotient space topology is a topological group.

We have only to show that the mapping  given by
given by  where
where 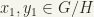 is continuous.
is continuous.
Let  be given by
be given by  where x, y are elements of G. We then have the following “loop”:
where x, y are elements of G. We then have the following “loop”:


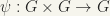

Trivially, we have 
Since  and
and 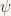 are continuous,
are continuous,  is also continuous. Hence,
is also continuous. Hence,  is continuous.
is continuous.
Let  be an open set in G/H. Then,
be an open set in G/H. Then, ![[\psi_{1}(\pi \times \pi)]^{-1}O_{1}](https://s0.wp.com/latex.php?latex=%5B%5Cpsi_%7B1%7D%28%5Cpi+%5Ctimes+%5Cpi%29%5D%5E%7B-1%7DO_%7B1%7D&bg=%23f6f5ed&fg=222222&s=0&c=20201002) is open in
is open in 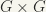 . But
. But  is open. Hence,
is open. Hence,
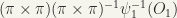 is open in
is open in  ; that is to say,
; that is to say, 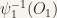 is open, hence
is open, hence  is continuous. QED.
is continuous. QED.

Let G be a topological group, and H a subgroup.
(a) If G is compact, then H and G/H are both compact.
(b) If G is locally compact, then both H and G/H are locally compact.

(a) H is a closed subset of a compact set, hence, compact, G/H is the continuous image of a compact set, hence, compact.
(b) H is locally compact since it is a closed subset of a locally compact space. [Let S be a locally compact space, 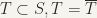 . Then T is locally compact. For,
. Then T is locally compact. For, 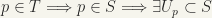 so that
so that  and
and 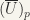 is compact. Now,
is compact. Now, 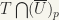 is a compact neighbourhood of p.]
is a compact neighbourhood of p.]
To prove that G/H is locally compact, let  , let
, let 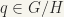 , and
, and  a neighbourhood of q, that is, an open set containing q.) Let
a neighbourhood of q, that is, an open set containing q.) Let
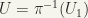
and let 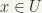 . so that
. so that  . Since G is locally compact, and U is open, there exists a neighbourhood O of x, such that
. Since G is locally compact, and U is open, there exists a neighbourhood O of x, such that 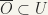 , with
, with  compact. [Let G be any topological group. To every neighbourhood U of e, there exists a neighbourhood V of e, such that
compact. [Let G be any topological group. To every neighbourhood U of e, there exists a neighbourhood V of e, such that  . For let V be a symmetric neighbourhood of e, such that
. For let V be a symmetric neighbourhood of e, such that  ]. (See (5) and (6) above). Now
]. (See (5) and (6) above). Now  . Hence,
. Hence,  , where
, where  . Therefore
. Therefore  . Hence,
. Hence,  . Then we have
. Then we have
 .
.
Since 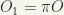 a neighbourhood of q(O is a neighbourhood of x). And,
a neighbourhood of q(O is a neighbourhood of x). And,  is compact. (since
is compact. (since  ). Since
). Since 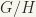 is a
is a  space,
space,  is closed.
is closed.
We have 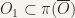 …..see above
…..see above 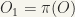 which implies that
which implies that  (compact).
(compact).
Hence,  is compact (closed subset of a compact set of a compact set). Thus,
is compact (closed subset of a compact set of a compact set). Thus, 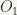 is a neighbourhood of q with compact closure. It follows that G/H is locally compact.
is a neighbourhood of q with compact closure. It follows that G/H is locally compact.

Let  denote the n-dimensional complex cartesian space. It is a vector space of dimension n over the field
denote the n-dimensional complex cartesian space. It is a vector space of dimension n over the field  of complex numbers.
of complex numbers.
Let ( where 1 is in the ith position. Then,
where 1 is in the ith position. Then,  form a basis of
form a basis of  over
over  .
.
An endomorphism  of
of  is defined when the elements
is defined when the elements  is equal to
is equal to  are given. To
are given. To  corresponds the matrix
corresponds the matrix 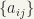 of degree n, and conversely.
of degree n, and conversely.
We use the same letter  for the matrix as well as the endomorphism.
for the matrix as well as the endomorphism.
We define a multiplication 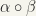 of two endos,
of two endos,  with matrics
with matrics 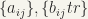 respectively by defining the corresponding matrix
respectively by defining the corresponding matrix  as the product of the matrices, namely
as the product of the matrices, namely
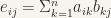
Now let  denote the set of all matrices of degree n with coefficients in
denote the set of all matrices of degree n with coefficients in  . If
. If  , put
, put 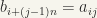 (as j goes from 1 to n, j-1 goes from 0 to n-1, and (j-1)n from zero to
(as j goes from 1 to n, j-1 goes from 0 to n-1, and (j-1)n from zero to  in steps of n, while i goes from 1 to n; so that i+(j-1)n goes from one to
in steps of n, while i goes from 1 to n; so that i+(j-1)n goes from one to 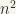 )
)
To  we associate the point with the coordinates
we associate the point with the coordinates  in
in 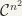 . In this way, we get a one to one correspondence between
. In this way, we get a one to one correspondence between  and
and 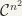 . Since
. Since 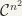 is a topological space, we define a topology in
is a topological space, we define a topology in  by requiring the correspondence to be a homeomorphism.
by requiring the correspondence to be a homeomorphism.
Let T be any topological space, and let  map T into
map T into  ;
;  . If
. If  ,
,  is a matrix with coefficients
is a matrix with coefficients  , say. Clearly,
, say. Clearly,  is continuous if and only if each function
is continuous if and only if each function 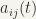 is continuous. Note that:
is continuous. Note that:
( ), where
), where  (In general, the following situation holds: If
(In general, the following situation holds: If  , then ” f is continuous iff
, then ” f is continuous iff  is continuous for *every*
is continuous for *every*  . On the one hand, it is trivial that : f continuous implies
. On the one hand, it is trivial that : f continuous implies  is continuous”. On the other, if
is continuous”. On the other, if  is continuous and *open*, with
is continuous and *open*, with  , then
, then 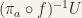 is open, that is,
is open, that is,  is open. But
is open. But  is open, since sets of the form
is open, since sets of the form  , U open, form a sub-basis of open sets of
, U open, form a sub-basis of open sets of  . So f is continuous).
. So f is continuous).
It follows from this remark, and (4.1) that the product  of two matrices
of two matrices 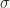 and
and  is continuous funcction of the pair
is continuous funcction of the pair  considered as a point of the space
considered as a point of the space  .
.
 We denote by
We denote by  the transpose of the matrix
the transpose of the matrix 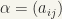 ;
; 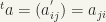 . We denote by
. We denote by  the complex conjugate of
the complex conjugate of  ;
; 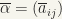 .
.
Clearly, 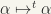 and
and  are homeomorphisms, of order 2, of
are homeomorphisms, of order 2, of  onto itself.
onto itself.
If  and
and  are any two matrices, then
are any two matrices, then  and
and 
An  matrix
matrix 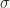 is regular (or non-singular), if it has an inverse, that is, if there exists a matrix
is regular (or non-singular), if it has an inverse, that is, if there exists a matrix 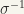 , such that
, such that  , where
, where  is the unit matrix of degree n.
is the unit matrix of degree n.
A necessary and sufficient condition for 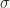 to be regular is that its determinant is non zero.
to be regular is that its determinant is non zero.
If an endomorphism 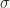 of
of  maps
maps  onto itself (and not some subspace of lower dimension) the corresponding matrix
onto itself (and not some subspace of lower dimension) the corresponding matrix 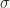 is regular, and
is regular, and 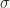 has a reciprocal endomorphism
has a reciprocal endomorphism 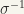 .
.
If 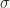 is a regular matrix, we have
is a regular matrix, we have
 = (^{t}\sigma)^{-1} and
= (^{t}\sigma)^{-1} and 
If 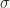 and
and  are regular matrices,
are regular matrices,  is also regular, and we have
is also regular, and we have
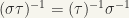 .
.
Hence, the regular matrices od degree n form a group with respect to multiplication, which is called the general linear group  .
.
Since the determinant of a matrix is obviously a continuous function (being a polynomial) of the matrix,  is an open subset of
is an open subset of  (
( ), det is a continuous function. ) The elements of
), det is a continuous function. ) The elements of  may be considered as points of a topological space which is a subspace of the topological space
may be considered as points of a topological space which is a subspace of the topological space  .
.
If  is a regular matrix, the coefficients
is a regular matrix, the coefficients  of
of 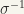 are given by
are given by  , where the
, where the  are polynomials in the coefficients
are polynomials in the coefficients 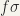 . Hence, the mapping of
. Hence, the mapping of  onto itself is continuous. Since the mapping coincides with its reciprocal mapping, it is a homeomorphism of
onto itself is continuous. Since the mapping coincides with its reciprocal mapping, it is a homeomorphism of  with itself.
with itself.
The mappings  and
and 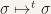 are also homeomorphisms of
are also homeomorphisms of  with itself. The first is an automorphism of the group, not the second (preserves sums and inverts the order of the products)
with itself. The first is an automorphism of the group, not the second (preserves sums and inverts the order of the products)
If 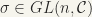 define
define 
Then, we have  and
and 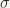
Thus, we have:  and
and  . Hence,
. Hence,  is a homeomorphism, and an automorphism of order 2 of
is a homeomorphism, and an automorphism of order 2 of  .
.
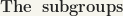 namely,
namely, 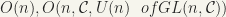
Let 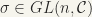 . We say that
. We say that 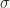 is orthogomal if
is orthogomal if  . The set of all orthogonal matrices of degree n we denote by
. The set of all orthogonal matrices of degree n we denote by  . If only
. If only 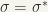 , then
, then 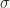 is called complex orthogonal, and the set of all such
is called complex orthogonal, and the set of all such 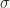 we denote by
we denote by  . If
. If 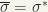 , then
, then 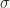 is called unitary, and we denote by
is called unitary, and we denote by  the set of all such
the set of all such 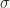 .
.
Since  and
and  are continuous, the sets
are continuous, the sets 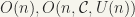 are closed subsets of
are closed subsets of  . [Note that
. [Note that  is closed if f is real and continuous.
is closed if f is real and continuous.  is continuouz for all i,j and
is continuouz for all i,j and  is closed]. Because these mappings are automorphisms,
is closed]. Because these mappings are automorphisms, 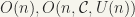 are subgroups of
are subgroups of  .
.
[Note, in parenthesis, that if X is any topological space, and Y a Hausdorff space, and f,g are continuous mappings of X into Y, then the set  is closed. One can see then the set E –
is closed. One can see then the set E –  is open in X. Let
is open in X. Let  . Since
. Since 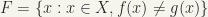 is open in X and …
is open in X and … , and Y is Hausdorff, there exist neighbourhoods
, and Y is Hausdorff, there exist neighbourhoods 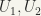 of
of  respectively so that
respectively so that  ). Since f and g are are continuous, there exist neighbourhoods
). Since f and g are are continuous, there exist neighbourhoods  of
of  in X such that
in X such that  . Let
. Let  . Then V is a neighbourhood of
. Then V is a neighbourhood of  , and
, and  for
for  , hence
, hence 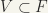 . It follows that F is open.]
. It follows that F is open.]
Clearly, 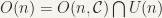 ….call this (i)
….call this (i)
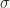 is real, if its coefficients are real, that is, if
is real, if its coefficients are real, that is, if 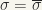 . The set of all real matrices of degree n we denote by
. The set of all real matrices of degree n we denote by  , and we define
, and we define  . Hence,
. Hence,  .
.
Since the determinant of the product of two matrices is the product of their determinants, the matrices of determinant I form a subgroup of  . The group of all matrices with determinant I in
. The group of all matrices with determinant I in  is called the special linear group
is called the special linear group 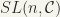 .
.
We set

 ….call this (ii)
….call this (ii)
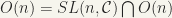 ….call this (iii)
….call this (iii)
Clearly,  are subgroups and closed subsets of
are subgroups and closed subsets of  . They may be considered as subspaces of
. They may be considered as subspaces of  .
.

 are compact.
are compact.
 We have only to show that
We have only to show that  is compact, since
is compact, since  are closed subsets of
are closed subsets of  . We shall see that
. We shall see that  is homeomorphis to a bounded, closed subset of
is homeomorphis to a bounded, closed subset of 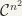 .
.
A matrix 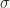 is unitary if and only if
is unitary if and only if 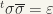 , where
, where  is the unit matrix. [
is the unit matrix. [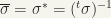 ]
]
If  . then
. then

[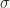 is regular, that is,
is regular, that is,  ]
]
The left hand side of the last equations are continuous functions of 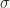 .
.  is not only a closed subset of
is not only a closed subset of  but also of
but also of  . [For
. [For  is an intersection of closed sets].
is an intersection of closed sets].
Further,
 for
for  .
.
Therefore the coefficients of the matrix 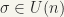 are bounded. Since
are bounded. Since 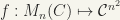 is a homeomorphism,
is a homeomorphism, 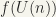 is closed and bounded, and a subset of
is closed and bounded, and a subset of 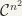 and hence compact.
and hence compact.
Cheere,
Nalin Pithwa
Mathematics Hothouse shares:
is true.
is true. The test criterion is then:
from the set of premises alone.